Java 面试总结四

2025-03-07

这部分主要是跟算法相关，包括加密、排序、遍历等。

加密

（1）下列哪些算法是对称加密？
A. MD5
B. RSA
C. DES
D. SHA

排序

（2）实现冒泡排序。

（3）实现快速排序。

遍历

（4）实现二叉树的先序、中序、后序遍历。

（5）编写一个方法，找出字符串中所有重复的字符。

问答

（6）红黑树的原理是什么？

（7）B+ 树的原理是什么？

参考答案

（1）C

常见的加密算法：

（一）单向加密：常见的都是基于 Hash 算法，哈希也叫散列，是一种将任意长度的消息/数据压缩到某一固定长度的消息摘要算法，只要输入数据有一点变化，那么生成的消息摘要就会有巨变。它还具有不可逆性，只能对明文进行加密得到密文，而不能通过密文反推出明文，比如：
MD5：使用时加盐，但存在‌哈希碰撞（哈希值长度固定为 128 位，不同的消息可产生相同的哈希值）；
SHA：比 MD5 更安全，常用的是 SHA-256。

（二）对称加密：使用同一个密钥进行加密和解密，比如：
DES：密钥长度较短（56 位），存在安全漏洞；
AES：比 DES 更安全，安全性最高的为 AES-256。

（三）非对称加密：使用两个不同的密钥进行加密和解密，一个公钥，一个私钥，用两者中的任意一个加密，就可以用另一个解密。比如：
RSA：安全性高，也需要较多的计算资源，可能在某些资源有限的场景下不太适用。它的加密和解密过程使用相同的算法，只是密钥的使用顺序不同，一般步骤为：公钥加密 -> 私钥解密；私钥签名 -> 公钥验签（加密是为了防止信息被泄露，签名是为了防止信息被篡改，证书是为了防止公钥 / 身份被假冒）。

加密算法和密钥的关系：算法是明确定义数据转换规则的数学过程，密钥是决定算法执行具体路径的动态参数，以加密过程为例，两者的协作可通过公式表达为：密文 = 算法（明文，密钥）。这种分离机制确保了即使算法被公开研究，只要密钥未泄露，就仍是安全的。

质数是很多加密算法的核心（利用大质数乘积难分解的特性）。质数是只能被 1 和它自身整除的数，快速判断数 n 是否为质数的方法为：检查从 2 到 √n 之间的整数是否存在能整除 n 的数，若不存在，则 n 为质数。

分解数 m 的质因数的方法为（质因数就是因数中的质数）：从最小质数 2 开始试除，若 m 能被 2 整除，则记录质因数 2，并将原数 m 除以 2 后再赋值给 m，重复此过程直到无法整除，接着换下一个质数 3 继续除，直到商为 1 为止（3 之后是 5、7、11……到 √m，若没有 ≤ √m 的质数能够整除，说明 m 本身为质数）：

private static List<String> factorize(int m) {
    List<String> factors = new ArrayList<>();
    // 处理偶数
    while (m % 2 == 0) {
        factors.add("2");
        m /= 2;
    }
    // 处理奇数因子（必须用质数试除，因为合数可分解为更小质数）
    for (int i = 3; i <= Math.sqrt(m); i += 2) {
        // 检查i是否为质数
        if (isPrime(i)) {
            while (m % i == 0) {
                factors.add(String.valueOf(i));
                m /= i;
            }
        }
    }
    // 剩余质数
    if (m > 2) {
        factors.add(String.valueOf(m));
    }
    return factors;
}

// 辅助方法：判断是否为质数
private static boolean isPrime(int num) {
    if (num <= 1) return false;
    if (num == 2) return true;
    if (num % 2 == 0) return false;
    for (int i = 3; i * i <= num; i += 2) {
        if (num % i == 0) return false;
    }
    return true;
}

（2）冒泡排序的思想是重复地遍历待排序数列，每次比较两个相邻的元素，如果顺序错误就交换，直到没有再需要交换的。实现代码如下：

public class BubbleSort {
    public static void sort(int[] arr) {
        int temp = 0;
        // 外层循环控制遍历次数
        for (int i = 0; i < arr.length - 1; i++) {
            // 内层循环控制每一轮的比较和交换
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
                }
            }
        }
    }
}

内层循环的范围会逐渐缩小，因为每一次遍历完后，最大的元素会「浮」到数组的末尾，所以在下一次遍历时，末尾的元素就不需要再比较了。优化点：添加一个布尔值标识遍历时是否发生交换，如果没有，说明数组已经有序，可以提前结束。

（3）快速排序采用分而治之的策略，其基本思想是先从待排序数组中选一个元素作为基准值，然后对数组分区，即将数组重新排列为两个子数组，一个子数组的元素都比基准值小，另一个子数组的元素都比基准值大，基准值处于中间位置，然后递归地对这两个子数组进行快速排序，从而使整个数组有序。实现代码如下：

public class QuickSort {
    /**
     * arr: 待排序数组
     * low: 数组的开始索引
     * high: 数组的结束索引
     */
    public static void sort(int[] arr, int low, int high) {
        if (low < high) {
            // pivotIndex 是分区后的基准位置
            int pivotIndex = partition(arr, low, high);
            // 递归基准左侧的子数组
            sort(arr, low, pivotIndex - 1);
            // 递归基准右侧的子数组
            sort(arr, pivotIndex + 1, high);
        }
    }
    
    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];// 选择最后一个元素作为基准
        int smallerIndex = (low - 1);// 假设把比基准值小的元素放在左侧，记录其位置
        for (int i = low; i < high; i++) {
            if (arr[i] < pivot) {
                smallerIndex++;// 增加较小元素的位置
                // 交换，将较小元素移到左侧
                int temp = arr[smallerIndex];
                arr[smallerIndex] = arr[i];
                arr[i] = temp;
            }
        }
        // 交换，将基准元素移到中间位置
        int temp = arr[smallerIndex + 1];
        arr[smallerIndex + 1] = arr[high];
        arr[high] = temp;
        return smallerIndex + 1;// 返回基准的正确位置
    }
    
    public static void main(String[] args) {
        int[] arr = {9, 2, 3, 1, 8, 5, 7, 6, 4, 0};
        sort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }
}

基准元素可以选择数组的第一个元素、最后一个元素、中间元素、随机元素或者三数取中等，选择合适的基准策略可以减少最坏情况的出现概率，从而提高算法的效率和性能。

（4）先序、中序、后序遍历是遍历二叉树的基本方法。
先序遍历的顺序是：根节点 -> 左子树 -> 右子树；
中序遍历的顺序是：左子树 -> 根节点 -> 右子树；
后序遍历的顺序是：左子树 -> 右子树 -> 根节点。
实现代码如下：

// 定义二叉树的节点类
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    public TreeNode(int val) {
        this.val = val;
    }
    // remaining omitted...
}

// 遍历算法类
public class TreeTraversal {
    
    // 先序遍历
    public static void preOrder(TreeNode root) {
        if (root == null) {return;}
        System.out.print(root.getVal() + " ");// 访问根节点
        preOrder(root.getLeft());// 递归访问左子树
        preOrder(root.getRight());// 递归访问右子树
    }
    
    // 中序遍历
    public static void inOrder(TreeNode root) {
        if (root == null) {return;}
        inOrder(root.getLeft());   // 递归访问左子树
        System.out.print(root.getVal() + " ");// 访问根节点
        inOrder(root.getRight());  // 递归访问右子树
    }
    
    // 后序遍历
    public static void postOrder(TreeNode root) {
        if (root == null) {return;}
        postOrder(root.getLeft());// 递归访问左子树
        postOrder(root.getRight());// 递归访问右子树
        System.out.print(root.getVal() + " ");// 访问根节点
    }
}

（5）方法如下：

public static void removeDuplicateChar(String str) {
    char[] charArr = str.toCharArray();
    Set set = new HashSet();
    for (char c : charArr) {
        if (!set.add(c)) {
            System.out.println("重复: " + c);
        }
    }
    System.out.println(set.toString());
}

（6）红黑树是自平衡的二叉查找树，数据分布在所有节点，通过颜色标记和旋转规则保持平衡‌。它在内存中操作高效，适用于需要频繁插入和删除操作的场景‌，比如 TreeMap、HashMap 和 Linux 的 epoll 机制等。下面介绍其原理，首先要知道二叉查找树（BST）的特征：

左子树上所有节点的值均小于或等于根节点的值；
右子树上所有节点的值均大于或等于根节点的值；
左、右子树也分别为二叉查找树。

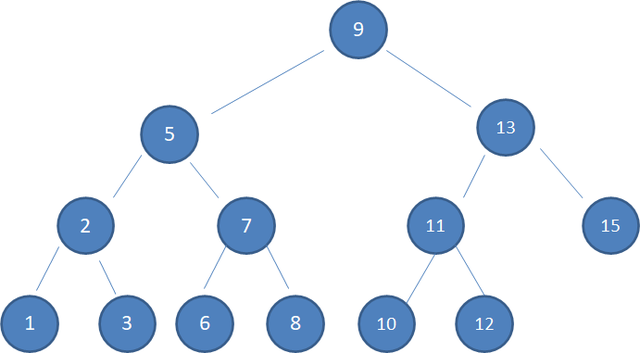
其查找过程类似二分法，查找所需的最大次数等同于二叉查找树的高度。但它在插入新节点时存在以下缺陷：

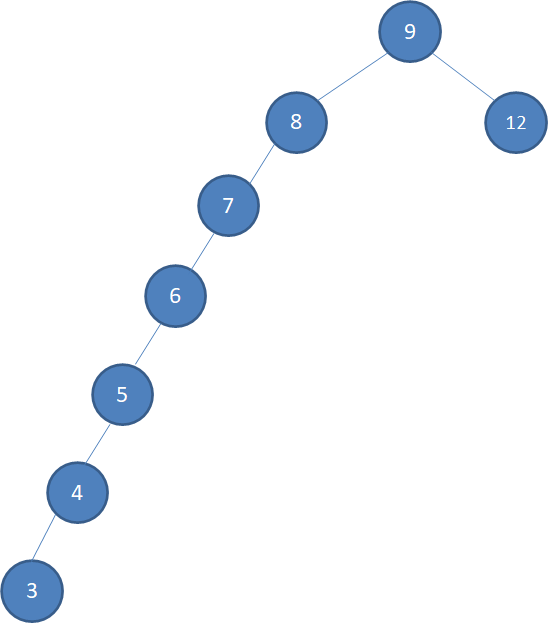
如果得到这种结构，那查找的性能将大打折扣，几乎变成了线性查找。为了解决这种失衡的情况，红黑树应运而生，它除了符合二叉查找树的基本特征外，还必须满足以下规则：（在使用红黑树之前，平衡的二叉查找树（AVL）也能解决失衡问题，它通过旋转来保证左右子树的深度差绝对值不超过 1，但这种相对严格的平衡条件导致插入数据时可能要进行大量的数据移动，虽然提高了查询性能，却损失了插入性能，红黑树的平衡条件相对宽松，在查询性能与插入性能之间实现了均衡）

每个节点非红即黑；
根节点必须是黑色；
所有叶子节点（空节点）视为黑色；
红色节点的子节点必须是黑色（‌不允许连续红色节点‌）；
从任意节点到其所有叶子节点的路径中，黑色节点数量相同（称为‌黑高‌，Black Height）。

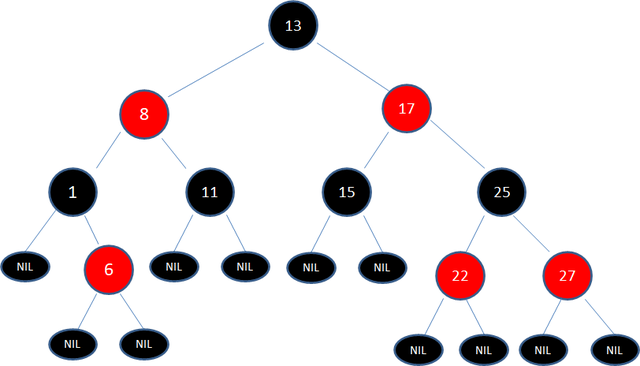
当插入或删除节点的时候，红黑树的规则有可能被打破，这时就需要通过变色（红色节点变为黑色，或黑色节点变为红色）和旋转（顺时针或逆时针旋转红黑树的两个节点）进行自我调整，使之重新满足所有规则。这些规则让红黑树能够保持整体的平衡状态，保证从根到叶子的最长路径不会超过最短路径的 2 倍，避免了极端情况下的低效操作。

（7）B+ 树是自平衡的多路查找树，所有数据存储在叶子节点并形成链表，数据是有序的，非叶子节点仅用于路由‌。适合磁盘存储，广泛应用于数据库索引和文件系统‌，其核心设计目标是减少磁盘 I/O 次数并支持高效的范围查询。首先还是来了解一下最原始的多路查找树（MST）的特征：

每个节点可以有多个子节点；
每个节点可以存储多个元素；
每个节点中的元素均按升序排列；
若节点包含元素 K1、K2，则左、中、右三个子树的元素值范围分别为（-∞，K1）、（K1，K2）、（K2，+∞）。

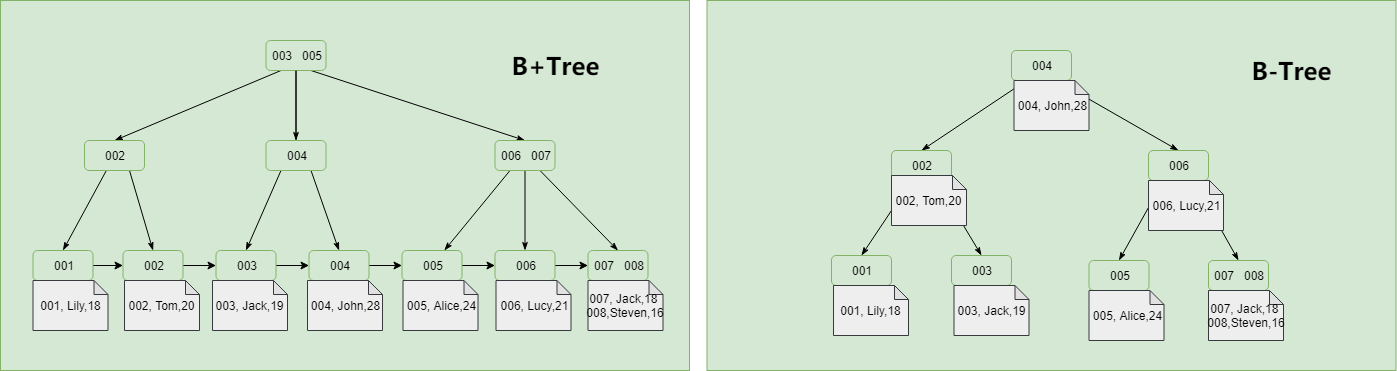
磁盘 I/O 是一个耗时操作，因为不管是从磁盘读数据到内存，还是从内存写数据到磁盘，通常要经过寻道、旋转和传输三个步骤，而树的高度会对 I/O 读写的次数造成直接影响，多路查找树的这种设计正好有效降低了树的高度，查询效率大大提高。B 树（也叫做 B-Tree，B 是 Balanced 的缩写）和 B+ 树都是多路查找树中的一种，下图是 B+ 树的结构：

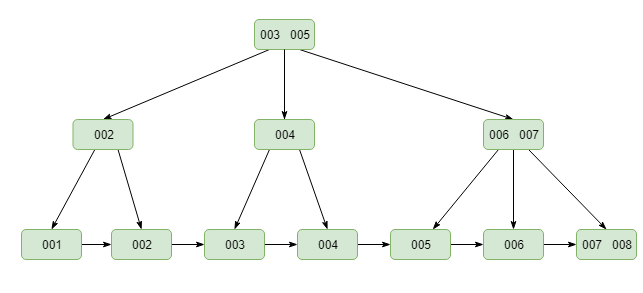
B+ 树与 B 树相比，在实现索引时主要有两个区别：

B+ 树只在叶子节点存储数据，非叶子节点只存储索引，而 B 树在叶子节点和非叶子节点都会存储数据；
B+ 树的叶子节点间通过指针链接，形成了一个双向的链表，通过遍历叶子节点即可获取所有数据（但单个叶子节点内部的数据是通过单向链表组织）。

B+ 树能存储的数据量也很大，Page 是 InnoDB 磁盘管理的最小单位，俗称数据页，默认大小为 16KB，每个 Page 对应 B+ 树的一个节点，那么 3 层的 B+ 树就可以存储 2 千万条左右的行记录，相当于 20G 左右。

B+ 树的自平衡通过节点的分裂和合并操作来维持，这里推荐一个数据结构的演示网站，在页面上找到 B+ 树后多操作几遍，理解会更加深刻。插入新数据时，通过逐层与非叶子节点的值作比较，找到待插入位置的叶子节点，然后自底向上插入，当节点变满时，进行分裂操作，删除数据时则可能又需要将节点合并。